发展氢能是我国向可再生零碳能源结构转型，实现“碳达峰、碳中和”目标的必由之路。可再生能源电解水制氢技术具有技术成熟、原料丰富、清洁低碳和安全高效等优点，备受研究者广泛关注。电解水制氢电极表面氢气泡生长及脱离等行为引发气泡局部微扰动，促进局部传质。同时，氢气泡在电极表面连续黏附，减小实际电化学活性反应面积，阻碍电极界面电子/离子传输，提高电极过电位和欧姆压降等，增大电解能耗、降低效率。因此，深入研究析氢电极表面气泡动力学规律对于突破电解水制氢能耗高、能量转化效率偏低等瓶颈问题至关重要。


为探明电解水制氢电极表面气泡动力学行为，诸多学者主要采用高速摄影可视化、电化学测量和理论分析等方法研究气泡生长、黏附和脱离等行为。当溶解氢分子浓度达到过饱和浓度条件时，电极表面成核点处产生气泡，随后气泡继续在电极表面生长和黏附。学术界主要采用理论分析结合电化学实验的方法研究电极表面气泡生长过程中的气液传质行为。当电极尺寸明显大于气泡直径时(常指宏观电极)，目前普遍认为气泡生长行为受气液界面扩散主导控制，并提出了相关气液界面扩散传质速率模型。而对于电极尺寸非常小的微电极表面，目前仅从理论上推测气泡生长行为受微液层直接注入控制。


宏观平面电极表面气泡成核点分布的随机性导致实验测量较为困难。近年来相关研究聚焦于微电极表面单个氢气泡行为，获得了较多微电极表面氢气泡动态生长过程中的气泡生长直径、生长时间及相关电化学实验数据，而针对气泡底部微液层结构及演变等数据非常匮乏。CHEN等通过理论分析，建立了基于相界面润湿动力学的气泡底部微液层模型；BASHKATOV等通过微电极实验，捕捉到气泡底部存在不稳定的微液层结构，认为微液层主要是由多个微小子气泡组成，微液层内的微小气泡群之间的聚并行为对气泡生长及脱离过程起到关键作用。此外，电解液欧姆热阻产生焦耳热，导致气液界面呈现电解液温度梯度分布，引发Marangoni对流效应，从而影响气泡生长和脱离等行为。微电极表面析氢气泡尺度非常小，目前仅靠实验研究难以深入揭示微液层结构和Marangoni对流效应的影响机制，而采用数值模拟手段能够细致描述和求解微尺度氢气泡周围温度场和速度场等信息。以往针对电极表面气泡生长行为数值模拟研究主要采用固定气泡直径模型。实际的气泡动态生长速度相对于Marangoni对流速度来说非常小，基于此探索若干不同气泡生长时刻对应不同直径的单个气泡周围多物理场信息及影响因素。CHEN等采用固定气泡直径模型研究电极表面气泡生长过程中Marangoni对流行为，但没有深入探究微电极体系考虑微液层结构对传热过程和温度场的影响，也没有深入研究单个连续气泡生长周期内Marangoni对流结构演变及影响规律。


本文作者基于前期获得的水平微电极表面单个氢气泡生长行为实验数据，采用固定气泡直径模型对实验电流密度条件下连续多个气泡生长时刻的不同直径气泡周围的Marangoni对流效应进行数值模拟，开发基于微液层模型的电场分布和传热过程计算方法，揭示气液界面温度场及Marangoni对流结构的演变规律。


1、计算模型及求解方法


1.1物理模型及网格划分


本文采用前期设计的水平微电极电解水制氢实验系统为参考物理模型，将水平铂微电极(直径为100μm)镶嵌在高硬度的环氧树脂玻璃平面中心，实验采用1.5 mol/L的H2SO4溶液作为电解液，在常温25℃环境下进行电解，在水平微电极表面周期性地产生单个氢气泡。为了尽量减少计算机耗时，并保证计算模拟的准确性，建立了以底部圆形微电极中心的法线为中心轴的三维圆柱几何模型，其直径为5 mm，高度为5 mm，实际电解实验系统尺寸远大于本文设计的计算区域尺寸。电极反应诱导产生的焦耳热主要在气泡表面附近电解液区域内传输，导致气液界面周围、特别是气泡底部区域产生温度梯度，从而仅主要在气液界面引发Marangoni对流效应。因此，本文仅对气泡周围局部区域的流动和传热过程进行模拟是可行的，设计的三维几何模型尺寸是合理的。实验中获得的气泡动态生长速度为0.01～1.00 mm/s，明显小于Marangoni对流速度(后文详细展示)，因此，本文采用固定气泡直径模型进行计算也是合理可靠的。


图1所示为局部放大显示的微电极表面单个氢气泡生长示意图。本文模拟设计的气泡半径Rb和气泡接触半径Rc来源于恒电流密度为5 A/cm2条件下的气泡几何尺寸实验，定义气泡弧长从气泡接触点开始到气泡顶点结束(图1中深蓝色弧线)，气泡接触角为θ，气液界面圆周角度为φ(φ≥θ)。计算区域的气泡底部微液层为圆柱结构，微液层底部直径与微电极直径相同。为简化求解，本文设计气泡底部平均微液层厚度为5μm。在实际电解过程中，气液界面和气泡底部微液层区域的物理场参数变化较大，为保证计算结果的准确性，需要对这2个区域进行网格加密处理。图2所示为三维圆柱模型中的气泡垂直中心截面和阴极底部面的网格划分和加密处理情况，从图2可见：气液界面和气泡底部微液层区域的网格非常小，气液界面最小网格尺寸为1.2μm，气泡底部微液层最小网格尺寸为0.5μm。

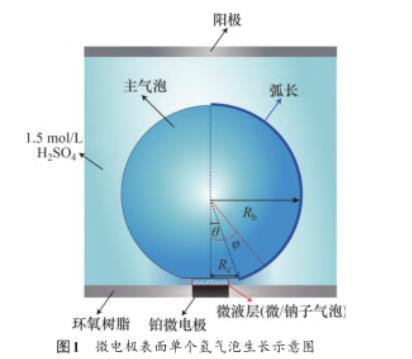
图1微电极表面单个氢气泡生长示意图

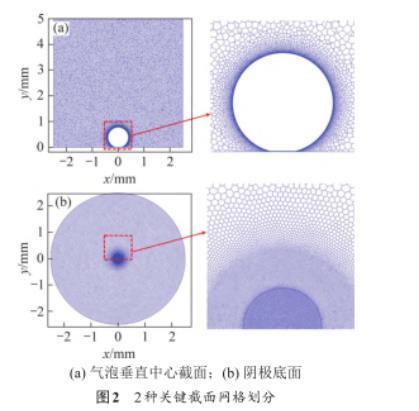
图2 2种关键截面网格划分


1.2数学模型及控制方程


电解水制氢体系内气泡周围的电解液流速较小，流动形态为明显的层流。电解液为不可压缩流体，描述单个氢气泡生长过程中的流体流动方程包括连续性方程和动量方程，采用Boussinesq假设来考虑电解液温度变化引起的浮力和自然对流过程，

式中：u为电解液速度；ρ为电解液密度；P为流体压力；μ为电解液黏度；g为重力加速度；t为时间；β为流体热膨胀系数；T为电解液温度；T0为初始环境温度(常温25℃)，相关模拟结果主要用电解液温度与初始环境温度的差值(即温度差)进行描述和讨论。


电解液欧姆热阻产生焦耳热传输过程，引发气液界面产生热Marangoni对流效应，描述单个气泡周围电解液温度变化的能量方程为


式中：λ为电解液导热系数；cp为电解液定压比热容；Sheat为焦耳热量源项，主要与局部电流密度和电导率有关。


电解过程的电势分布通过拉普拉斯方程进行求解，电流密度分布由电势梯度和局部电导率进行求解，


式中：φ为电解电势；j为电解电流密度；κm为局部混合电导率，与局部区域的纯电解液电导率κ和气体含量αg有关，其计算公式为


气泡周围区域和微液层区域的电解液电导率不同，其中气泡周围为纯电解液，而微液层内几乎为大量的微/纳米子气泡组成，仅有少量的电解液，因此微液层区域的混合相电导率非常小，不考虑电解液电导率的温度补偿效应的影响。根据计算的局部电流密度和混合相电导率，计算得到焦耳热源项


1.3边界条件及求解方法


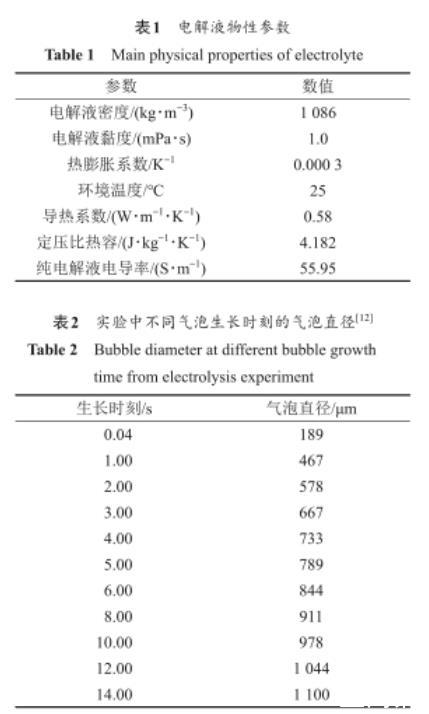
对于考虑Boussinesq假设的电解液自然对流过程，为了提高计算收敛稳定性，采用非稳态迭代方法进行计算，当监测的气液界面若干位置处的温度和速度保持不变，即认为计算过程达到收敛。定义微电极表面为实际实验的电流密度，定义阳极表面为压力出口。将气液界面定义为热Marangoni对流边界条件，表面张力随温度变化的系数为-1.5×10-4N/(m·K)，其他壁面定义为无滑移壁面边界条件。采用用户自定义标量函数UDS求解槽内电势分布，混合相电导率和焦耳热源项均采用了用户自定义函数UDF进行编程计算。计算过程中的连续性方程和动量方程均采用二阶迎风格式，能量方程和UDS方程采用Quick格式，压力-速度耦合采用Phase-Coupled SIMPLE算法，所有计算方程的松弛因子均采用默认值，时间步长为1 ms。模拟所需的电解液物性参数如表1所示，微液层内气体的体积分数约为94%，计算得到微液层混合相电导率为2.28 S/m。为了系统研究气泡生长周期内气泡周围Marangoni对流效应的演变规律，对不同气泡生长时刻对应的不同气泡尺寸模型进行数值模拟，结果如表2所示。


自古以来，数学家们都致力于揭示现象背后的本质，牛顿作为人类历史上最伟大的数学家和物理学家之一，他利用数学解释物理现象，并且创立了微积分。数学模型可以解释事物背后的隐蔽模式，今天数学家和应用者们从实际中提炼出数学问题，再寻找合适的数学算法来解题，从而建立模型，这些模型可以应用到复杂、多变的自然现象、人类行为、社会系统等问题，微积分让我们能够更加深刻认识实数的性质，认识世界的本质。微积分的诞生极大地推动了力学、光学、热学等各个领域的科技发展，促进了现代学科专业的发展。