热线:021-56056830,66110819
手机:13564362870


热线:021-56056830,66110819
手机:13564362870
在本节中,我们首先介绍在空气呼吸燃料电池极化扫描期间同时获得的I–V、温度、PO2、RH和PH2O数据。然后,我们展示了在固定电流负载条件下,从阴极表面的垂直z和水平y横向获得的温度、PO2和RH分布。最后,我们讨论了由突然电流中断周期引起的电压、温度、PO2和RH的瞬态响应。
电流-电压极化。-图6显示了空气呼吸燃料电池的I–V极化扫描,同时测量了位于燃料电池阴极表面(y=0 mm,z=1.6 mm)上方的mi)微型传感器单元的温度、PO2、RH和PH2O响应。测量期间的环境实验室条件为:塔姆比安=21°C,环境=44%。随着电流密度的增加,微传感器在阴极表面附近记录到显著的热加热、氧气消耗和水生成。尽管图6中的大多数趋势都是直观的,但相对湿度响应值得讨论。随着电流密度的增加,相对湿度最初略有上升,然后在最高电流密度下略有下降。当结合温度读数并转换为PH2O值时,这些相对湿度的趋势最容易理解。如图所示,PH2O随电流的增加而线性增加。近表面相对湿度表示膜的欧姆性能,而PH2O值表示阴极的净质量传输速率。在高电流密度下,PH2O增加(表明反应速率增加),但较高的温度意味着相对湿度下降(饱和水蒸汽压随温度呈指数增加),见上文等式3。后者导致膜阻力显著增加,从而导致细胞电位下降。当电流密度高于350 mA/cm2时尤其如此,此时温度对相对湿度的影响占主导地位,电池电位急剧下降。我们的吸气式燃料电池模型捕捉到了PH2O和RH与电流密度之间的这些趋势。19
根据电流密度和反应物消耗(或产物生成)之间的线性对应关系,预计PO2随电流密度的增加而线性减少,而PH2O随电流密度的增加而线性增加。假设传感器探头位于扩散层内,简单的流量平衡产生以下线性关系:
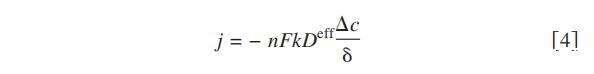
这里j是电流密度,n是反应数,F是法拉第常数,Deff是有效扩散率,Δc是扩散层上浓度的变化,δ是特征扩散层厚度,k是阴极集电器未阻挡的活性面积分数。仅基于图6难以提取关于阴极扩散层的进一步细节。然而,如下文所述,通过分析空间变化和瞬态响应,可以获得该过程的进一步细节(包括Deff和δ的估计值)。
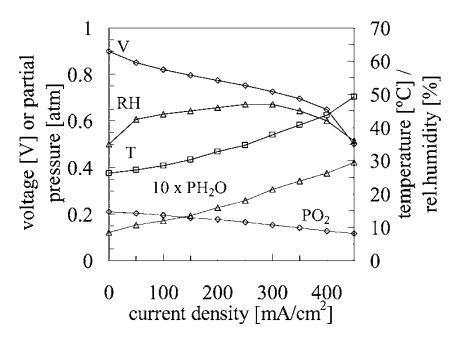
图6.在标准极化扫描过程中,测量电压、温度、相对湿度、PO2和PH2O作为平面空气呼吸燃料电池电流密度的函数。
轮廓(Z和Y)扫描。-图7显示了从燃料电池阴极表面的Y横向(水平)测量中提取的测量温度和PO2轮廓,Z=1.6 mm,Y=-1.52至1.52 mm,增量为254µm,工作电流密度为222和444 mA/cm2。图8提供了从第二组y导线中提取的RH和PH2O剖面,从y=z=1.6 mm处−1.52至1.52 mm,增量为508μm,且操作点相同。由于通道肋的存在,PO2剖面表现出强烈的影响,而RH和PH2O剖面受肋的影响较小。温度分布几乎与肋的位置无关,这很可能是由于肋的高导热性。通过这些测量,我们可以推断出氧、水蒸气和温度扩散层的相对尺寸。我们假设,受肋骨位置强烈影响的标量场表示具有与肋骨特征尺寸相当或更小的特征长度的较小扩散层。
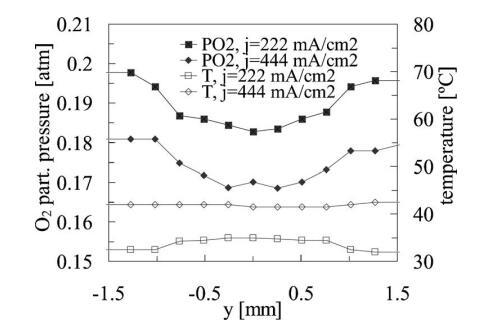
图7.在距离y=1.6 mm的z=1.6 mm处,测量温度和氧分压PO2,作为传感器组件位置的函数−对于222和444 mA/cm2的两个电流密度负载,1.52至y=1.52 mm。
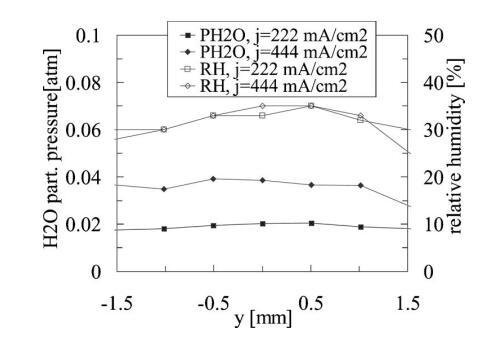
图8.在距离y=1.6 mm的z=1.6 mm处,测量水蒸气分压(PH2O)和相对湿度(RH),作为传感器组件位置的函数−对于222和444 mA/cm2的两个电流密度负载,1.52 mm到y=1.52 mm。
正如预期的那样,更高的电流密度操作点会导致更高的温度、更大的氧气消耗和更大的水输出(如温度曲线中的最大值、PO2曲线中的最小值以及j=444 mA/cm2时的PH2O曲线中的最大值所示)。同时,较高的电流密度操作点导致PO2、PH2O和温度随y的相对变化减小。这些趋势与扩散层厚度随电流密度的增加而增加是一致的。有趣的是,相对湿度随电流密度的变化很小。较大的电流密度会增加局部产品的水蒸气,但伴随较大的温度,因此相对湿度大致不变。
图9提供了在相同的两个工作电流密度下,从燃料电池阴极通道底部开始的z-横向测量中提取的温度和PO2分布图。图10提供了从第二组z-导线在相同操作点提取的RH和PH2O剖面,但从顶部阴极肋表面平面(z=1.5 mm)开始。温度、PO2、RH和PH2O都显示出对z位置的强烈依赖性。有趣的是,它们都表现出长程行为,梯度延伸到阴极表面以上几毫米。我们通过距离δ95%(在z方向)量化扩散层的范围,在该距离处,测量的固相或温度的局部值和环境值之间的差值下降到z=0时初始值的5%。在222和444 mA/cm2条件下,扩散层厚度的估算值为:水蒸气分压为4.5和5.4 mm,氧分压为4.3和6.1 mm,tem)温度为7.4和9.4 mm。这些剖面图表明,呼吸空气燃料电池阴极处的质量传输扩散层可能比之前假设的空间范围大得多。20,21我们强调,在这些实验中,应特别注意尽可能保护燃料电池免受外部对流气流的影响(为了表征自然对流对传质的贡献,降低传感器噪音,提高再现性)。封闭房间中的气流可以显示比自然对流诱导气流(9–11 cm/s9)更高的速度值因此,这些实验条件可能代表受控静态环境的“最坏情况”情景。因此,此处给出的y和z曲线可能对应于扩散层大小和影响的上限。在实际的空气呼吸燃料电池环境中(例如,在办公大楼中),外部对流可能会减少该扩散层的空间范围。
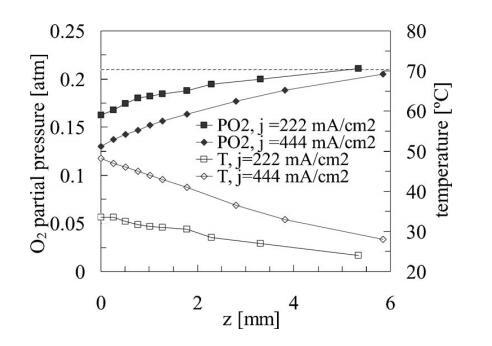
图9.对于222和444 mA/cm2的两个电流密度负载,在y=0 mm时,在z=0 mm到z=6 mm的范围内测量氧分压和温度,作为传感器组件位置的函数。虚线显示了环境氧气浓度。
燃料电池阴极表面/环境界面处的有效氧和水扩散系数(DO2 eff和DH eff 2O)可根据方程式4的通量平衡模型进行估算,如图9和图10中测量的空间O2和H2O分布。拟合这些空间剖面的初始斜率(从z=0到z=1mm),其中平面扩散近似最有可能成立,得到0.14–0.26 cm2/s的DO2 eff估计值和0.21–0.38 cm2/s的DH eff 2O估计值。这些估算值代表了有效扩散率,其中包含了对流效应(如有),这将增强质量传输。DO2 eff和DH eff 2O值与公布的298 K]T]330 K时空气中氧的自由扩散系数DO2值(0.24–0.29 cm2/s)和空气中水蒸气的自由扩散系数DH2O值的顺序相同,对于298 K]T]330 K.22,0.26–0.30 cm2/s的扩散率测量值与公布值之间的差异可能是由于自然对流、阴极通道中的非平面扩散以及湿度探头有限体积导致的相对湿度测量不确定性的影响,实际布拉格光栅温度和热电偶读数之间的差异等。作为上述简单扩散分析的替代方法,我们在此给出传质系数的估算值。为此,我们使用以下通量平衡方程描述对流传质
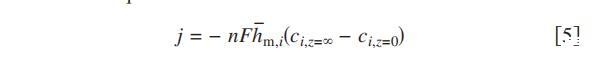
此处“hm,i是spe)的平均对流传质系数i(cm/s),ci,z=0是物种i在z=0时的浓度,ci,z=是物种i的环境浓度。在我们之前的模型19中获得的氧和水蒸气传质系数和值的估计值汇总在表I中。
表I.在222和444 mA/cm2电流密度下,本研究中获得的平均水蒸气和氧气对流传质系数与通过组合传质和传热模型(见参考文献19)获得的值之间的比较。
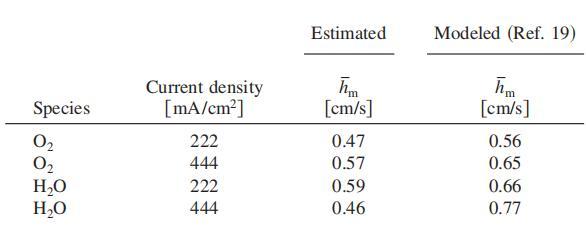
对于20°C和45%相对湿度的类似负载和环境条件,氧传质的估算值与我们的近期建模结果一致。在444 mA/cm2的较高电流密度下估算的水蒸气传质系数与模型预测不同。我们将此归因于水蒸气浓度估计的测量不确定度,因为阴极表面的水蒸气浓度是从阴极肋上方测量的温度和相对湿度值推断出来的。
与质量通量不同,阴极表面的热流必须视为对流和辐射分量的总和,如以下热流方程所示
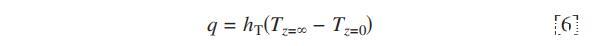
这里hT是总传热系数,可以表示为对流传热系数hTc和辐射传热系数hTr之和。辐射传热系数定义为
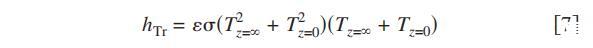
式中, 是表面发射率, 是波尔兹曼常数,Tz=0是z=0时的温度,Tz=是环境温度。
表II将从图9所示温度剖面获得的对流和辐射平均传热系数的估计值与从我们之前的建模中获得的值进行了比较。19我们假设阴极表面为灰色,发射率为0.9,并且是等温的。用于计算产生热量的燃料电池电压在222 mA/cm2的电流负载下为0.75 V,在444 mA/cm2的电流负载下为0.63 V。燃料电池阴极产生的热量不仅取决于燃料电池的电压和电流,还取决于凝结水的比例,并将凝结潜热添加到热流平衡中。根据我们之前的实验研究9,我们假设大约30%的产品水在我们的实验中冷凝。估算值与我们的模型预测值吻合良好,相差约10%。
表二。在222和444 mA/cm2的两种电流密度负载下,估算和模拟(见参考文献19)平均传热系数的比较。对于所有估计,我们假设阴极表面为等温灰色,表面发射率为0.9。我们还假设约30%的生成水已凝结(见参考文献9)。
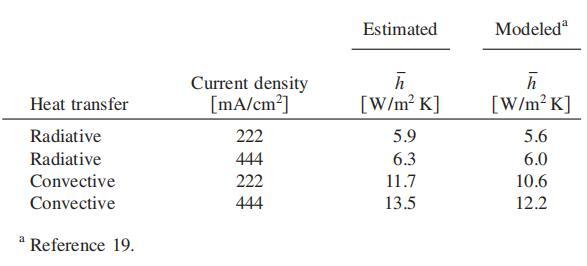
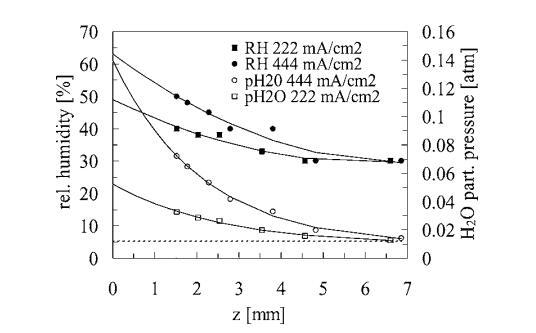
图10. 对于222和444 mA/cm2的两个电流密度负载,在z=1.5 mm到z=7 mm之间的z移动期间,测量相对湿度和部分水蒸汽压,作为传感器组件的函数。记录的相对湿度和温度(未显示)读数(填充标记)用二阶多项式拟合近似(实线并外推至z=0。根据实际测量值确定的水蒸气浓度显示为空标记,而实线显示的水蒸气浓度是通过使用二阶多项式近似温度和相对湿度获得的。虚线显示的是环境水蒸气浓度在实验过程中(21°C和45%相对湿度)的温度变化。
瞬态测量。-图11a显示了在0和333 mA/cm2之间的电流中断脉冲周期内记录的电压、温度和PO2瞬态。在图11a的比例下,约375 s时发生的电压瞬态很难解析,因此图11b中提供了放大版本。图11b中的氧瞬态。11b可适用于时间常数为τO2-6 s的单指数模型。此短的单时间常数可能与边界层中的O2扩散有关。相反,温度瞬态需要同时适用于指数项和线性项。指数项(τT-20 s)可能与燃料电池体的热质量以及热边界层的形成有关。线性项(-0.19°C/min)是由于阴极表面的持续浸没导致气体扩散层中的传质损失,从而导致电池电位降低,并增加热量产生。如果液态水从阴极表面持续去除,则线性项为ab)。23
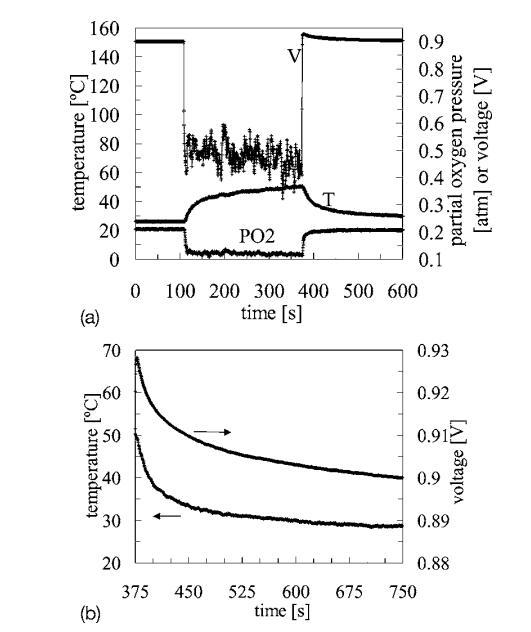
图11.(a)在0和333 mA/cm2之间的阶跃电流脉冲期间,温度、燃料电池电压和氧分压随时间变化的测量,传感器组件位于z=0 mm和y=0 mm处。(b)t=375 s电流转换后的温度和电压瞬态详情。
鉴于测得的氧浓度随时间变化的恢复率,可使用瞬态扩散标度参数估计燃料电池阴极扩散层内的有效氧扩散率。对于一阶,扩散瞬态遵循众所周知的标度关系
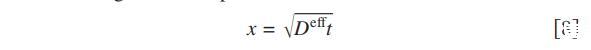
其中,x是与横向扩散过程相关的特征长度标度,Deff是有效扩散率,t是时间。使用从z剖面分析(x=δO2=0.6 cm)获得的扩散层估计值,我们可以从公式8中提取有效氧扩散率的粗略估计值。该分析产生DO2 eff~0.06 cm2/s。该估算值类似,但略小于从先前通量平衡分析中获得的值-应用于图9中空间O2分布的等式4]。我们得出结论,由于固有传感器响应限制,瞬态技术可能略微低估了真实的氧气扩散率(见测量程序一节)。测得的O2瞬态弛豫时间(tO2-6 s)与固有O2传感器速度(tO2传感器-1.3 s)相当,导致O2瞬态信号“仪器展宽”。使用较小毛细管直径的O2微传感器可以提高传感器速度,但会增加噪声并降低传感器稳定性。
图12显示了在相同电流负载循环条件下(0和333 mA/cm2之间)测得的RH和PH2O瞬态。当RH信号显示非常小的瞬态响应时,PH2O响应在恒流负载下显示较大的变化。PH2O瞬态的初始部分可近似为指数,产生时间常数τH2O-14 s。该时间常数基本上反映了湿度传感器的上升时间,因此无法准确测量初始PH2O变化的时间尺度,但我们可以将其值限制在约14 s以内。随后随时间变化的PH2O增加速度要慢得多,本质上是非指数性的。该响应表明如前所述,液态水在阴极表面积聚。当电流在t-1500秒中断时,PH2O很快恢复到环境条件,松弛时间约为14秒。(然而,这一次,请注意,PH2O信号不包含二次线性分量。)另一方面,相对湿度响应显示出有趣的超调行为。这种超调很可能与湿度传感器固有响应时间的限制有关(请参阅湿度传感器校准部分)。为了完整起见,我们注意到,这种超调也可能是由产水立即中断和电池温度缓慢下降之间的时间延迟造成的。由于这种滞后,阴极上方仍然温暖的空气将经历相对湿度的突然下降,这可能会随着电池(和周围空气)冷却而重新覆盖。
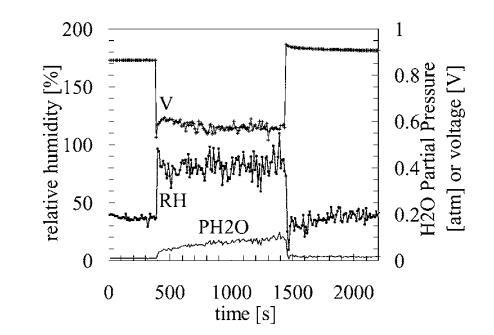
图12.(a) 在0和333 mA/cm2之间的阶跃电流脉冲期间,测量相对湿度、燃料电池电压和水蒸气分压随时间的变化,传感器组件位于z=1.6 mm和y=0 mm处。